Rétro-ingénierie d'une station météo

TL;DR : Le code est disponible sur GitHub : https://github.com/AntoineVe/Otio_WH510

Pour recevoir les signaux de la station météo, j'utilise une radio définie par logiciel, ou software defined radio.

La radio Définie par logiciel, ou SDR pour Software Definied Radio, consiste à utiliser un ordinateur et une suite logicielle pour recevoir/émettre, moduler/démoduler, crypter/décrypter des signaux Radio. La pratique s'est développée dans les années 90 avec le perfectionnement du matériel informatique.
– La Radio Définie par Logiciel (SDR) avec le chipset rtl2832u

Le signal est émis sur 868,292 Mhz. J'ai donc utilisé la commande suivante pour recevoir le signal : rtl_433 -f 868292000 -q -A.

Voici un exemple des données reçues :

$ rtl_433 -f 868292000 -q -A
 Found Rafael Micro R820T tuner
 Exact sample rate is: 250000.000414 Hz
 Sample rate set to 250000.
 Bit detection level set to 0 (Auto).
 Tuner gain set to Auto.
 Tuned to 868292000 Hz.
 Detected OOK package    @ 2017-07-31 01:05:40
 Analyzing pulses...
 Total count:   79,  width: 38949                (155.8 ms)
 Pulse width distribution:
  [ 0] count:   37,  width:   123 [121;127]      ( 492 us)
  [ 1] count:   42,  width:   367 [365;368]      (1468 us)
 Gap width distribution:
  [ 0] count:   78,  width:   243 [241;245]      ( 972 us)
 Pulse period distribution:
  [ 0] count:   36,  width:   366 [364;370]      (1464 us)
  [ 1] count:   42,  width:   610 [608;612]      (2440 us)
 Level estimates [high, low]:  15881,      2
 Frequency offsets [F1, F2]:   -1699,      0     (-6.5 kHz, +0.0 kHz)
 Guessing modulation: Pulse Width Modulation with fixed gap
 Attempting demodulation... short_limit: 245, long_limit: 246, reset_limit: 246, demod_arg: 0
 pulse_demod_pwm(): Analyzer Device
 bitbuffer:: Number of rows: 1
 [00] {79} fe bc 64 74 bc 02 04 21 d4 f2
 
 ^CSignal caught, exiting!
 
 User cancel, exiting...

La ligne qui nous interresse ici est [00] {79} fe bc 64 74 bc 02 04 21 d4 f2. Pour information, la station est à environ 20m du récepteur.

Vient ensuite le moment d'analyser cette suite hexadécimale. Pour cela, j'ai laissé tourner l'enregistrement des données reçues (une redirection de la sortie de rtl_433 vers un fichier). J'ai ainsi pu voir quelles parties de la chaîne se modifiaient dans la journée. Pour une mieux visualiser ces données, j'ai écrit un script python utilisant pylab et numpy. Ce script prend en argument le fichier écrit par rtl_433 et affiche un graphique.

meteo_graph.py

#!/bin/python3
 
from sys import argv
from pylab import *
import numpy as np
 
data_file = argv[1]
 
 
def col2array(dico, col):
    temp_liste = list()
    for line in dico:
        temp_liste.append(int(dico[line][col], 16))
    return(np.array(temp_liste))
 
 
with open(data_file, 'r') as data:
    data = data.read().splitlines()
data_dict = {}
count = 0
for line in data:
    if "[00] {79}" in line:
        data_dict.update({count: tuple(line.replace('[00] {79} ','').split())})
        count += 1
x = np.array(list(data_dict.keys()))
y0 = col2array(data_dict, 0)
y1 = col2array(data_dict, 1)
y2 = col2array(data_dict, 2)
y3 = col2array(data_dict, 3)
y4 = col2array(data_dict, 4)
y5 = col2array(data_dict, 5)
y6 = col2array(data_dict, 6)
y7 = col2array(data_dict, 7)
y8 = col2array(data_dict, 8)
y9 = col2array(data_dict, 9)
 
figure(figsize=(21,10), dpi=100)
# plot(x, y0, label="col 0")
# plot(x, y1, label="col 1")
plot(x, y2, label="col 2 (temp)")
print('temp1 : ', y2)
plot(x, y3, label="col 3 (temp)")
print('temp2 : ', y3)
plot(x, y4, label="col 4 (hum)")
print('hum : ', y4)
plot(x, y5, label="col 5 (vent ?)")
plot(x, y6, label="col 6 (vent ?)")
plot(x, y7, label="col 7 (pluie ?)")
plot(x, y8, label="col 8 (?)")
# plot(x, y9, label="col 9")
legend(loc='best')
# savefig("/tmp/meteo-graph.svg", dpi=100)
show()
close('all')

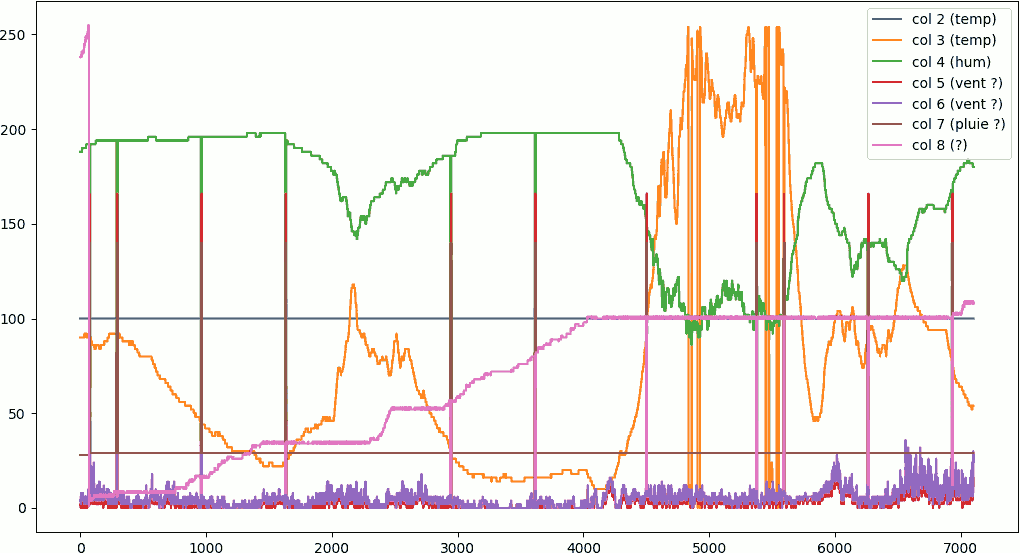
J'ai ensuite rapproché les relevés bruts avec les données affichées sur le terminal météo fourni. Après avoir un peu tâtonné, l'analyse tend vers une relation linéaire entre données reçues et données affichées. Pour cette analyse numérique, je vais faire de la régression linéaire.

Avec python, c'est la fonction linregress du module stats de scipy qui va me servir.

linregress(x, y=None)
    Calculate a linear least-squares regression for two sets of measurements.

    Parameters
    ----------
    x, y : array_like
        Two sets of measurements.  Both arrays should have the same length.
        If only x is given (and y=None), then it must be a two-dimensional
        array where one dimension has length 2.  The two sets of measurements
        are then found by splitting the array along the length-2 dimension.

    Returns
    -------
    slope : float
        slope of the regression line
    intercept : float
        intercept of the regression line
    rvalue : float
       correlation coefficient
    pvalue : float
        two-sided p-value for a hypothesis test whose null hypothesis is
        that the slope is zero.
    stderr : float
        Standard error of the estimated gradient.

Pour la température, j'ai pu déduire que c'était sur les octets 3 et 4 que l'information était codée (e.g. [00] {79} fe bc 64 74 bc 02 04 21 d4 f2, ici 0x64 et 0x74). L'information est donc codée sur 4 octets.

Régression linéaire :

>>> from scipy import stats
>>> raw_data = [25776, 25780, 25790, 25794, 25796, 25798]
>>> real_data = [20, 20.2, 20.7, 20.9, 21, 21.1]
>>> a, b, r, p, std_err = stats.linregress(raw_data, real_data)
>>> a,b
(0.050000000000000031, -1268.8000000000006)
>>> std_err
0.0
>>>

On a donc : f(x) = 0,05 * x − 1268,8. Avec une erreur standard nulle, ce qui signifie que la formule « tombe juste » (Si on trace la courbe à partir de la formule, elle passe parfaitement par tous les points relevés).

En python :

>>> def temp(data):
...  return round((0.05*data-1268.8), 1)
...
>>> temp(0x6474)
17.0

J'ai également remarqué que l'état des piles modifie l'offset de la formule, j'ai donc ajouté un dictionnaire permettant d'intervertir les valeurs quant c'est nécessaire.

Pour l'humidité, j'ai identifié les changements sur le 5ème octet. On voit bien sur la courbe des relevés la relation qu'ont la température et l'humidité. L'analyse numérique donne a = 0,5 et b = 0, avec également une erreur standard nulle. La relation est donc très simple : y = 0.5 * x. C'est à dire que la valeur de l'humidité est la donnée (convertie en entier décimal) divisée par deux.

En python :

   >>> def hum(data):
   ...  return int(round(data/2))
   ...
   >>> hum(0xbc)
   94

La station météo renvoie deux paramètres pour le vent : une moyenne (ou médiane ?) et le maximum (ce qui correspond aux rafales). Ceux-ci sont portés sur les octets 6 et 7. L'analyse numérique :

>>> from scipy import stats
>>> raw = [0x00, 0x02, 0x04, 0x06, 0x08, 0x0a, 0x0c, 0x0e, 0x10, 0x12, 0x14, 0x16, 0x1c, 0x22, 0x24, 0x28, 0x2e, 0x50, 0x5a]
>>> read = [0, 1.1, 2.5, 3.6, 5.0, 6.1, 7.2, 8.6, 9.7, 11.2, 12.2, 13.3, 17.3, 20.9, 22, 24.5, 28.1, 49, 55.1]
>>> a, b, r, p, std_err = stats.linregress(raw, read)
>>> a, b
(0.61264343715451175, -0.018142655636458116)
>>> std_err
0.0009343564466014815
>>>

J'ai essayé avec les différentes configuration : km/h, mph, knots (nœuds), … Jamais d'erreur standard nulle mais c'est avec les km/h qu'elle est le plus faible (0.00093). Certainement une erreur à cause d'arrondis.

La fonction est donc :

>>> def wind(data):
...  return round((0.61264343715451175*data-0.018142655636458116),1)
...
>>> wind(0x5a)
55.1

Pour le pluviomètre, il n'y a pas de formule. C'est un compteur : à chaque fois qu'il s'incrémente de 2 unités, il faut ajouter 0,3 mm de pluie. La donnée est codée sur 1 octet, le 8ème de la transmission, et donc overflow à 0xFF. Il faut pouvoir gérer cette situation. Pour plus de facilité, je stocke la valeur dans un fichier temporaire.

def rain(raw):
     current = int(raw)
     try:
         with open("/tmp/old_rain", "r") as tmp:
             old_rain = int(tmp.read())
     except FileNotFoundError:
         old_rain = None
     except Exception as err:
         logging.error("Error : " + str(err))
         return int(0)
     if old_rain is None:
         with open("/tmp/old_rain", "w") as tmp:
             tmp.write(str(current))
         return int(0)
     if current > old_rain:
         res = round(float(current-old_rain)*0.3, 1)
         with open("/tmp/old_rain", "w") as tmp:
             tmp.write(str(current))
     else:
         if (current+255)-old_rain < 254:
             res = round(float((current+255)-old_rain)*0.3, 1)
             with open("/tmp/old_rain", "w") as tmp:
                 tmp.write(str(current))
         else:
             res = 0
     return float(res)